
Standar deviasi adalah konsep statistika yang memainkan peran penting dalam mengukur sejauh mana data tersebar dari nilai rata-rata. Dalam artikel ini, kita akan menjelaskan apa itu standar deviasi, bagaimana menghitungnya, dan pentingnya dalam menganalisis keragaman data.
1. Definisi Standar Deviasi:
Standar deviasi adalah ukuran statistika yang mengukur sejauh mana set data tersebar dari nilai rata-rata. Semakin tinggi standar deviasi, semakin besar variasi atau dispersi data. Sebaliknya, semakin rendah standar deviasi, semakin mendekati nilai rata-rata.
2. Cara Menghitung Standar Deviasi:
Langkah-langkah umum untuk menghitung standar deviasi adalah sebagai berikut:
- Hitung nilai rata-rata (mean) dari data.
- Kemudian, hitung selisih antara setiap nilai data dan nilai rata-rata.
- Kuadrat setiap selisih.
- Hitung rata-rata dari kuadrat selisih tersebut.
- Ambil akar kuadrat dari rata-rata tersebut.
Rumus standar deviasi (σ) dapat diwakili sebagai berikut:
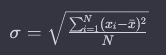
3. Interpretasi Standar Deviasi:
– Jika standar deviasi rendah, data cenderung berkumpul dekat dengan nilai rata-rata, menunjukkan kurangnya variasi.
– Jika standar deviasi tinggi, data tersebar lebih luas dari nilai rata-rata, menunjukkan tingkat variasi yang tinggi.
4. Pentingnya Standar Deviasi:
– Mengukur Ketersebaran Data: Standar deviasi memberikan gambaran tentang seberapa besar atau kecil ketersebaran data. Ini membantu dalam mengevaluasi apakah data cenderung berkumpul di sekitar nilai rata-rata atau memiliki variasi yang signifikan.
– Analisis Risiko dan Ketidakpastian: Dalam keuangan dan ilmu sosial, standar deviasi digunakan untuk mengukur risiko dan ketidakpastian. Semakin tinggi standar deviasi dalam saham atau harga aset, semakin besar risikonya.
– Pembanding Kinerja: Dalam pengukuran kinerja atau eksperimen ilmiah, standar deviasi digunakan untuk membandingkan tingkat variasi di antara kelompok atau kondisi.
5. Contoh Penggunaan Standar Deviasi:
Misalkan kita memiliki dua set data yang mewakili hasil ujian dua kelas berbeda. Meskipun kedua kelas memiliki rata-rata yang sama, kita dapat menggunakan standar deviasi untuk menentukan apakah ada variasi yang signifikan dalam kinerja siswa di setiap kelas.
6. Batasan Standar Deviasi:
Saat menggunakan standar deviasi, perlu diingat bahwa itu dapat dipengaruhi oleh nilai ekstrem atau outliers dalam data. Sebagai alternatif, deviasi mutlak atau interquartile range dapat digunakan untuk mengatasi batasan ini.
Kesimpulan:
Standar deviasi adalah alat statistik yang kuat dalam menganalisis dan memahami sebaran data. Dengan memahami konsep ini, para peneliti, analis data, dan pengambil keputusan dapat membuat interpretasi yang lebih baik tentang karakteristik dan keragaman data, membantu dalam pengambilan keputusan yang lebih informasional dan akurat.