- Kalkulator
- Teks aljabar linier pengantar
Kadang-kadang perlu untuk menemukan vektor bukan nol yang, ketika dikalikan dengan matriks bujur sangkar, akan menghasilkan kelipatan dari vektor tersebut. Vektor bukan nol ini disebut “vektor eigen”. Vektor eigen tidak hanya menarik bagi matematikawan, tetapi juga bagi orang lain dalam profesi seperti fisika dan teknik. Untuk menghitungnya, Anda perlu memahami aljabar matriks dan determinan.
Pelajari dan pahami definisi “vektor eigen”. Ditemukan untuk matriks kuadrat nxn A dan juga nilai eigen skalar yang disebut “lambda”. Lambda diwakili oleh huruf Yunani, tetapi di sini kita akan menyingkatnya menjadi L. Jika ada vektor bukan nol x dengan Ax = Lx, vektor x ini disebut “nilai eigen dari A”.
Temukan nilai eigen matriks dengan menggunakan persamaan karakteristik det (A — LI) = 0. “Det” adalah determinan, dan “I” adalah matriks identitas.
Hitung vektor eigen untuk setiap nilai eigen dengan mencari ruang eigen E(L), yang merupakan ruang nol dari persamaan karakteristik. Vektor bukan nol dari E(L) adalah vektor eigen dari A. Ini ditemukan dengan memasukkan kembali vektor eigen ke dalam matriks karakteristik dan mencari basis untuk A — LI = 0.
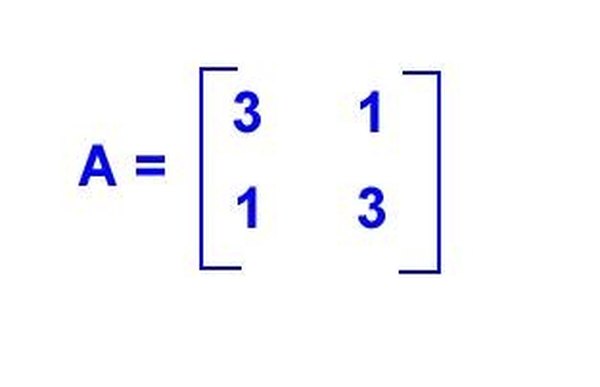
Latih Langkah 3 dan 4 dengan mempelajari matriks di sebelah kiri. Ditampilkan adalah matriks persegi 2 x 2.
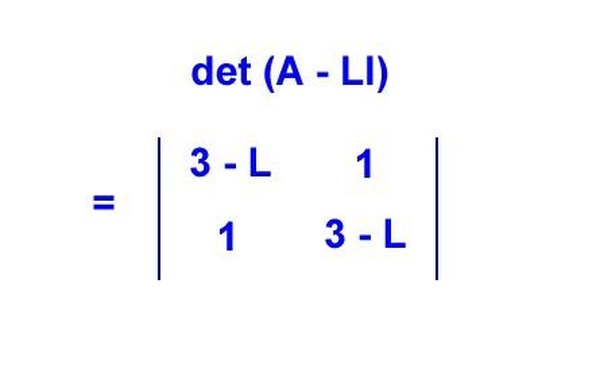
Hitung nilai eigen dengan menggunakan persamaan karakteristik. Det (A — LI) adalah (3 — L)(3 — L) –1 = L^2 — 6L + 8 = 0, yang merupakan polinomial karakteristik. Memecahkan ini secara aljabar memberi kita L1 = 4 dan L2 = 2, yang merupakan nilai eigen dari matriks kita.
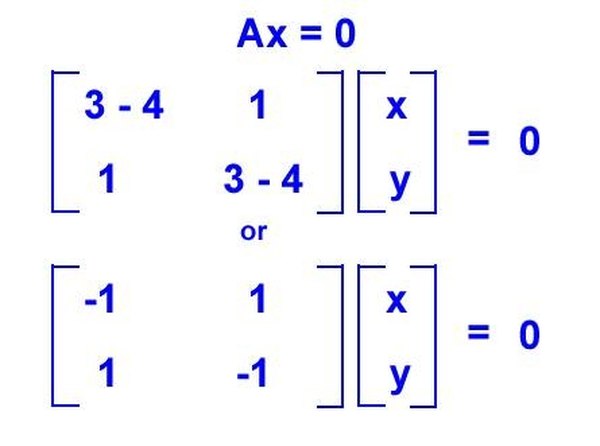
Temukan vektor eigen untuk L = 4 dengan menghitung ruang nol. Lakukan ini dengan menempatkan L1 = 4 dalam matriks karakteristik dan mencari basis untuk A — 4I = 0. Selesaikan ini, kita temukan x — y = 0, atau x = y. Ini hanya memiliki satu solusi independen karena sama, seperti x = y = 1. Oleh karena itu, v1 = (1,1) adalah vektor eigen yang merentang ruang eigen dari L1 = 4.
Ulangi Langkah 6 untuk mencari vektor eigen untuk L2 = 2. Kita temukan x + y = 0, atau x = –y. Ini juga memiliki satu solusi independen, katakanlah x = –1 dan y = 1. Oleh karena itu v2 = (–1,1) adalah vektor eigen yang merentang ruang eigen dari L2 = 2.
 Lyudmil Antonov Lantonov
Lyudmil Antonov Lantonov





