Hasil kali dua besaran skalar adalah skalar, dan hasil kali skalar dengan vektor adalah vektor, tetapi bagaimana dengan hasil kali dua vektor? Apakah itu skalar, atau vektor lain? Jawabannya adalah, bisa juga!
Ada dua cara untuk mengalikan vektor secara bersamaan. Salah satunya adalah dengan mengalikan perkalian titiknya, yang menghasilkan skalar, dan yang lainnya dengan mengalikan perkalian silangnya, yang menghasilkan vektor lain. Produk mana yang akan digunakan bergantung pada skenario tertentu dan berapa jumlah yang Anda cari.
titik terkadang disebut sebagai perkalian skalar atau perkalian dalam . Secara geometris, Anda dapat menganggap perkalian titik antara dua vektor sebagai cara mengalikan nilai vektor yang hanya menghitung kontribusi arah yang sama.
- Catatan: Produk titik mungkin negatif atau positif, tetapi tanda itu bukan indikasi arah. Meskipun dalam satu dimensi, arah vektor sering ditunjukkan dengan tanda, besaran skalar juga dapat memiliki tanda yang terkait dengannya yang bukan merupakan indikator arah. Utang hanyalah salah satu dari banyak contoh ini.
Definisi Produk Dot
Hasil kali titik vektor a = (a x , a y ) dan b = (b x , b y ) dalam sistem koordinat kartesius standar didefinisikan sebagai berikut:
bold{acdot b} = a_xb_x + a_yb_y
Saat Anda mengambil produk titik dari sebuah vektor dengan dirinya sendiri, hubungan yang menarik akan muncul:
bold{acdot a} = a_xa_x + a_ya_y = |bold{a}|^2
Dimana | sebuah | adalah besar (panjang) dari a oleh teorema Pythagoras.
Rumus perkalian titik lainnya dapat diturunkan dengan menggunakan hukum kosinus. Ini dilakukan sebagai berikut:
Pertimbangkan vektor bukan nol a dan b bersama dengan vektor selisihnya a – b . Susunlah ketiga vektor tersebut hingga membentuk segitiga.
Hukum cosinus dari trigonometri memberi tahu kita bahwa:
|bold{ab}|^2 = |bold{a}|^2 + |bold{b}|^2 – 2|bold{a}||bold{b}|cos(theta )
Dan dengan menggunakan definisi produk titik kita mendapatkan:
|bold{ab}|^2 = (bold{ab})cdot (bold{ab}) = (a_x-b_X)^2 + (a_y-b_y)^2\ = (a_x)^2 + (b_x)^2 – 2a_xb_x + (a_y)^2 + (b_y)^2 – 2a_yb_y\ = |bold{a}|^2 + |bold{b}|^2 – 2bold{a cdot b}
Mengatur kedua ekspresi sama dan kemudian menyederhanakan, kita mendapatkan:
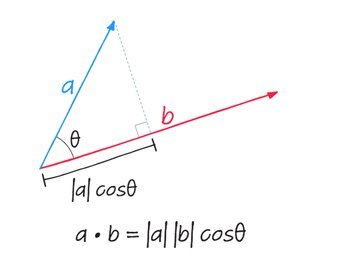
batal{|bold{a}|^2} + batal{|bold{b}|^2} – 2bold{a cdot b} = batal{|bold{a}|^2 } + batal{|bold{b}|^2} – 2|bold{a}||bold{b}|cos(theta)\text{ }\menyiratkan boxed{ bold{a cdot b} = |bold{a}||bold{b}|cos(theta)}
Formulasi ini memungkinkan intuisi geometris kita ikut bermain. Besaran | a |cos(θ) adalah besarnya proyeksi vektor a ke vektor b .
Jadi kita dapat menganggap produk titik sebagai proyeksi satu vektor ke vektor lainnya, dan kemudian produk dari nilainya. Dengan kata lain, itu dapat dilihat sebagai produk dari satu vektor dengan jumlah vektor lain dalam arah yang sama dengan vektor itu sendiri.
Properti Produk Dot
Berikut adalah beberapa properti produk dot yang mungkin berguna bagi Anda:
#Teks 1. Jika } theta = 0text{, maka } bold{a cdot b} = |bold{a}||bold{b}|
Ini karena cos(0) = 1.
\teks{2. Jika } theta = 180text{, maka }bold{a cdot b} = -|bold{a}||bold{b}|
Ini karena cos(180) = -1.
\teks{3. Jika } theta = 90text{, maka } bold{a cdot b} = 0
Ini karena cos(90) = 0.
- Catatan: Untuk 0 <
SAYA
< 90, perkalian titik akan positif, dan untuk 90 <
SAYA
< 180, perkalian titik akan negatif.
\teks{4. } bold{acdot b} = bold{bcdot a}
Ini mengikuti dari penerapan hukum komutatif ke definisi perkalian titik.
\teks{5. } bold{acdot (b+c)} = bold{acdot b} + bold{acdot c}
Bukti:
bold{acdot (b+c)} = bold{a}cdot(b_x + c_x, b_y + c_y) \ =a_x(b_x + c_x) + a_y(b_y + c_y)\ = a_xb_x + a_xc_x + a_yb_y + a_yc_y \ = (a_xb_x + a_yb_y) + (a_xc_x + a_yc_y)\ = bold{acdot b} + bold{acdot c} #text{6. } c(bold{acdot b}) = (cbold{a})cdot bold{b}
Bukti:
c(bold{acdot b}) = c(a_xb_x + a_yb_y)\ = ca_xb_x + ca_yb_y\ = (ca_x)b_x + (ca_y)b_y\ = (cbold{a})cdot tebal{b}
Cara Menemukan Produk Dot
Contoh 1: Dalam fisika, usaha yang dilakukan oleh gaya F pada benda saat mengalami perpindahan d , didefinisikan sebagai:
W=bold{F}cdot bold{d} = |bold{F}||bold{d}|cos(theta)
Dimana θ adalah sudut antara vektor gaya dan vektor perpindahan.
Besarnya usaha yang dilakukan oleh suatu gaya merupakan indikasi seberapa besar kontribusi gaya tersebut terhadap perpindahan. Jika gaya searah dengan perpindahan (cos(θ) = 0), gaya tersebut memberikan kontribusi maksimumnya. Jika tegak lurus dengan perpindahan (cos( Ѳ ) = 90), tidak memberikan kontribusi sama sekali. Dan jika berlawanan dengan perpindahan, (cos(θ) = 180), kontribusinya negatif.
Misalkan seorang anak mendorong kereta mainan melintasi lintasan dengan menerapkan gaya 5 N pada sudut 25 derajat terhadap garis lintasan. Berapa usaha yang dilakukan anak tersebut di atas kereta api ketika dia memindahkannya sejauh 0,5 m?
Larutan:
F = 5 text{ N}\ d = 0.5text{ m}\ theta = 25degree\
Dengan menggunakan definisi produk dot dari kerja, dan memasukkan nilai, kita kemudian mendapatkan:
W = Fdcos(theta) = 5times0.5timescos(25) = boxed{2.27text{ J}}
Dari contoh konkrit ini, seharusnya lebih jelas lagi bahwa penerapan gaya yang tegak lurus terhadap arah perpindahan tidak akan berhasil. Jika anak mendorong kereta pada sudut yang tepat ke lintasan, kereta tidak akan bergerak maju atau mundur di sepanjang lintasan. Juga intuitif bahwa usaha yang dilakukan oleh anak di kereta api akan bertambah dengan berkurangnya sudut dan gaya serta perpindahan mendekati kesejajaran.
Contoh 2: Daya adalah contoh lain besaran fisik yang dapat dihitung menggunakan perkalian titik. Dalam fisika, daya sama dengan kerja dibagi waktu, tetapi juga dapat ditulis sebagai perkalian titik gaya dan kecepatan seperti yang ditunjukkan:
P = frac{W}{t} = frac{bold{Fcdot d}}{t} = bold{F}cdot frac{bold{d}}{t} = bold{ Fcdot v}
Dimana v adalah kecepatan.
Perhatikan contoh anak sebelumnya bermain dengan kereta api. Sebaliknya, jika kita diberi tahu bahwa gaya yang sama diterapkan menyebabkan kereta bergerak dengan kecepatan 2 m/s ke bawah lintasan, maka kita dapat menggunakan perkalian titik untuk mencari daya:
P = bold{Fcdot v} = Fvcos(theta) = 5times2timescos(25) = 9.06text{ Watt}
Contoh 3: Contoh lain di mana produk titik digunakan dalam fisika adalah dalam kasus fluks magnet. Fluks magnet adalah jumlah medan magnet yang melewati area tertentu. Ini ditemukan sebagai produk titik dari medan magnet B dengan luas A. (Arah vektor luas adalah normal , atau tegak lurus, terhadap permukaan luas.)
Phi=bold{Bcdot A}
Misalkan medan sebesar 0,02 Tesla melewati lingkaran kawat dengan jari-jari 10 cm, membuat sudut 30 derajat dengan garis normal. Apa itu fluks?
Phi=bold{Bcdot A} = BAcos(theta) = 0.02times(pitimes0.1^2)timescos(30) = 0.000544text{ Wb}
Ketika fluks ini berubah, baik dengan mengubah nilai medan, mengubah luas loop atau mengubah sudut dengan memutar loop atau sumber medan, arus akan diinduksi dalam loop, menghasilkan listrik!
Sekali lagi perhatikan bagaimana sudut itu relevan dengan cara yang intuitif. Jika sudutnya 90 derajat, ini berarti medan akan terletak di sepanjang bidang yang sama dengan luas dan tidak ada garis medan yang melewati loop, sehingga tidak ada fluks. Jumlah fluks kemudian meningkat semakin dekat sudut antara medan dan garis normal menjadi 0. Produk titik memungkinkan kita untuk menentukan seberapa besar medan dalam arah normal ke permukaan, dan karenanya berkontribusi pada fluks.
Proyeksi Vektor dan Produk Dot
Pada bagian sebelumnya, telah disebutkan bahwa perkalian titik dapat dianggap sebagai cara untuk memproyeksikan satu vektor ke vektor lainnya dan kemudian mengalikan besarannya. Dengan
demikian, tidak mengherankan jika rumus untuk proyeksi vektor dapat diperoleh dari perkalian titik.
Untuk memproyeksikan vektor a ke vektor b , kita ambil perkalian titik a dengan vektor satuan ke arah b , lalu kalikan hasil skalar ini dengan vektor satuan yang sama.
Vektor satuan adalah vektor dengan panjang 1 yang terletak pada arah tertentu. Vektor satuan dalam arah vektor b hanyalah vektor b dibagi dengan besarnya:
frac{bold{b}}{|bold{b}|}
Jadi proyeksi ini kemudian:
text{Proyeksi }bold{a}text{ ke }bold{b} = Besar(bold{a}cdotfrac{bold{b}}{|bold{b}|} Besar)frac{bold{b}}{|bold{b}|} = Besar(bold{a}cdotfrac{bold{b}}{|bold{b}|^ 2}Besar)bold{b}
Produk Dot dalam Dimensi Lebih Tinggi
Sama seperti vektor yang ada dalam dimensi yang lebih tinggi, begitu pula perkalian titik. Bayangkan contoh anak mendorong kereta lagi. Misalkan dia mendorong ke bawah dan ke samping ke sisi lintasan. Dalam sistem koordinat standar, vektor gaya dan perpindahan perlu direpresentasikan sebagai tiga dimensi.
Dalam n dimensi, perkalian titik didefinisikan sebagai berikut:
bold{acdot b} = overset{n}{underset{i=1}{sum }}a_ib_i = a_1b_1 + a_2b_2 +…+ a_nb_n
Semua sifat perkalian titik yang sama dari sebelumnya masih berlaku, dan hukum cosinus sekali lagi memberikan hubungan:
bold{a cdot b} = |bold{a}||bold{b}|cos(theta)
Di mana besarnya setiap vektor ditemukan melalui yang berikut, sekali lagi konsisten dengan teorema Pythagoras:
|bold{a}|=sqrt{bold{acdot a}}=sqrt{(a_1)^2+(a_2)^2+…+(a_n)^2}
Cara Menemukan Perkalian Titik dalam Tiga Dimensi
Contoh 1: Perkalian titik sangat berguna saat perlu mencari sudut antara dua vektor. Misalnya kita ingin menentukan sudut antara a = (2, 3, 2) dan b = (1, 4, 0). Bahkan jika Anda membuat sketsa kedua vektor tersebut dalam 3-ruang, akan sangat sulit untuk membungkus kepala Anda di sekitar geometri. Tapi matematika cukup mudah, dengan menggunakan fakta bahwa:
bold{a cdot b}=|bold{a}||bold{b}|cos(theta)\menyiratkan theta=cos^{-1}Besar(frac{ tebal{acdot b}}{|bold{a}||bold{b}|}Besar)
Kemudian hitung perkalian titik a dan b :
bold{acdot b}=2times1+3times4+2times0=14
Dan menghitung besaran masing-masing vektor:
|bold{a}|=sqrt{2^2+3^2+2^2}=sqrt{17}=4.12\|bold{b}|=sqrt{1^2+4^ 2+0^2}=sqrt{17}=4.12
Dan akhirnya memasukkan semuanya, kita mendapatkan:
theta=cos^{-1}Besar(frac{bold{acdot b}}{|bold{a}||bold{b}|}Besar)=cos^{- 1}Besar(frac{14}{4,12times 4,12}Besar)=kotak{34,4derajat}
Contoh 2: Muatan positif berada di titik koordinat (3, 5, 4) dalam ruang tiga dimensi. Pada titik manakah sepanjang garis yang menunjuk ke arah vektor a = (6, 9, 5) medan listrik terbesar?
Solusi: Dari pengetahuan kita tentang bagaimana kekuatan medan listrik berhubungan dengan jarak, kita tahu bahwa titik pada garis yang paling dekat dengan muatan positif adalah lokasi di mana medan akan menjadi yang terkuat. Dari pengetahuan kita tentang produk dot, kita mungkin menduga bahwa penggunaan rumus proyeksi masuk akal di sini. Rumus itu seharusnya memberi kita vektor yang ujungnya tepat pada titik yang kita cari.
Kita perlu menghitung:
text{Proyeksi }(3, 5, 4)text{ ke }bold{a}=Big((3,5,4)cdotfrac{bold{a}}{|bold{ a}|^2}Besar)bold{a}
Untuk melakukannya, pertama, mari temukan | a | 2 :
|bold{a}|^2=6^2+9^2+5^2=142
Maka perkalian titik:
(3,5,4)cdot (6,9,5)=3times6+5times9+4times5=83
Membagi ini dengan | a | 2 menghasilkan 83/142 = 0,585. Kemudian mengalikan skalar ini dengan a memberikan:
0,585bold{a}=0,585 kali (6,9,5)=(3,51,5,27,2,93)
Oleh karena itu, titik di sepanjang garis di mana medan paling kuat adalah (3.51, 5.27, 2.93).
 Dan Chen | Sains
Dan Chen | Sains





